İNTERNET OKUL

Üçgen, doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimidir.

Düzlem geometrisinin temel şekillerinden biridir. Bir üçgenin üç köşesi ve bu köşeleri birleştiren, doğru parçalarından oluşan üç kenarı vardır. Bir Üçgenin iç açılarının toplamı 180° dış açılarının toplamı 360°'dir.

$[A B] U [A C] U [B C] = A B C$

Burada;

A, B, C noktaları üçgenin köşeleri ve $[A B],[A C],[B C]$ doğru parçaları üçgenin kenarlarıdır.

Üçgenin açıları

BAC, ABC ve ACB üçgenin içaçılarıdır.

$| B C | = a$ , $| A B | = c$ ve $| A C | = b$

$α$ + $β$ + $γ$ =180°

1. Üçgenin iç açıları toplamı 180 derecedir. Bir ABC üçgenine, A tepe noktasından teğet geçecek ve BC ye paralel olacak şekilde bir doğru çizildiğinde, BC doğru parçasının açıları, iç ters açılar kuralından dolayı tepe açısının yanına gelerek bir doğru parçasının yarısını kaplarlar.

2. Üçgende bir dış açı, kendisine komşu olmayan iki iç açının toplamına eşittir. Bir ABD üçgenine, D tepe noktasından teğet geçecek ve taban olan BC ye paralel olacak şekilde bir doğru çizilip kenarlar uzatıldığında, yöndeş açılar kuralı yardımıyla bu önerme kanıtlanabilir.

Üçgenlerin türleri

Üçgenler, kendilerini oluşturan parçaların (köşe, kenar, açılar vb.) aynı düzlemde olup olmadığına göre sınıflandırılabilir. Eğer üçgenin tamamı tek bir düzlemdeyse düzlemsel, diğer durumlarda da örneğin küresel ya da hiperbolik üçgen terimleri kullanılır.

Üçgen çeşitleri:

Eş Kenar Üçgen

Eşkenar üçgen

Tüm kenarları eşit olan üçgendir. Tüm iç açıları 60°'dir.

İkiz Kenar Üçgen

İkizkenar üçgen

İki kenarı eşit olan üçgenlerdir.

Çeşit Kenar Üçgen

Her kenarının uzunluğu farklı olan üçgenlerdir. Tüm iç açıları birbirinden farklıdır.

Dar Açılı Üçgen

90°'den küçük açılara sahip üçgenlerdir. Dik Açılı Üçgen

Açıları dik (90°) olan üçgenlerdir.

Geniş Açılı Üçgen

Açılarında biri 90°'den geniş olan üçgenlerdir.Sadece bir tek kenarı geniş açı olabilir

Üçgen Bağıntıları

Pisagor Bağıntısı

Bir dik üçgenin dik kenarlarına 'a' ve 'b' dersek hipotenüs'ün karesi bu kenarların uzunluklarının karelerinin toplamına eşittir. Yani:
$a 2 + b 2 = c 2$ . Buna Pisagor Teoremi denir

Öklid Bağıntısı

$| A B | 2 = | B H | . | B C |$
$| A C | 2 = | C H | . | B C |$
$| A H | 2 = | B H | . | C H |$

Alan Hesaplaması

Kenardan Yararlanma

Alan hesaplaması

Bir üçgenin alanı taban ve tabana ait yüksekliğin çarpımının yarısıdır:

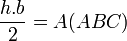
$frac{h.b}{2}=A(ABC)$

Açıdan Yararlanma

Bir üçgenin alanı, iki kenarın ve bu kenarların arasında kalan açının sinüsünün çarpımının yarısıdır:

Heron Yöntemi

Çevre uzunluğuna 2u, yarısına u dersek alan:

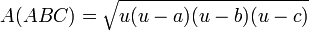
$A(ABC)=sqrt{u(u-a)(u-b)(u-c)}$

Kosinüs Teoremi

Herhangi bir üçgende a, b, c kenarlarını alalım. a ve b arasında kalan açı da alfa( $α$ ) olsun. c kenarını bulmak için kullanılacak formül:

$c=sqrt{a^2+b^2-2ab.cosalpha}$

Üçgende Yardımcı Elemanlar [

Açıortay

Bir açıyı iki eş açıya bölen doğru veya doğru parçasına açıortay denir.

$frac{|AC|}{|CD|}=frac{|AB|}{|DB|}$

Açıortay Uzunluğu

$|AD|=sqrt{|AC||AB|-|BD||DC|}$

Kenarortay

Kenarortaylar ve ağırlık merkezi

Bir üçgende bir köşeden karşısındaki kenara uzatılan doğru bu kenarı iki eş parçaya bölüyorsa buna kenarortay denir.Bir üçgende kenarortayların kesiştiği noktaya ağırlık merkezi denir. G harfi ile gösterilir. Ağırlık merkezi, bir kenarortayı $2 n$ ve $n$ olarak böler. Yani köşeye A, kenarortayın kenarı kestiği noktaya D dersek;
$| A G | = 2 | G D |$ olur.

Kenarortay teoremi

$2V^2_a=b^2+c^2-frac{a^2}{2}$